PASS User Manual
Contents
|
1 Short Description
PASS can be used to analyze
concurrent probabilistic programs which map to Markov decision processes.
By means of predicate abstraction and abstraction refinement,
PASS scales to very large finite state spaces and even infinite-state models
far beyond the reach of numerical methods which operate
on the full state space of the model.
The computational engines we use are SMT solvers to compute finite abstractions,
numerical methods to compute probabilities on these abstractions,
and interpolation as part of abstraction refinement.
PASS has been successfully applied to network protocols
and serves as a test platform for different refinement methods.
Here we give an overview of how to use
PASS, in particular how to set
parameters that influence the operation of its computational engines
and input/output behavior.
2 Usage
PASS is invoked from the command line with
input files and program options as parameters.
Input files and program options can be specified in arbitrary order (if there are conflicting options
the option that comes last takes effect).
Properties can be specified in separate files or contained in the same
file as the model.
In addition, there are program options to control the behavior of the different components of
the tool, as well as verbosity, graph output and debugging outputs.
All options are discussed in detail in the following sections.
2.1 Abstraction Refinement
2.1.1 Refinement Strategy
| --Strategy=[Configuration] | Specify a strategy for abstraction refinement |
The refinement strategies differ in the way predicates are synthesized to refine the abstraction.
For details about these methods, please refer to our publications.
The following strategies are available in PASS:
Configuration |
Description |
strongestEvidence |
Refinement as in [HermannsWZ08] |
anyDiff |
Refinement inspired by [KattenbeltKNP09] |
optDiff |
Refinement as in [WachterZ10] |
onlyScheduler |
Refinement only based on deviation between schedulers (no path checking) |
2.1.2 Selection of interpolating decision procedure
| --Interpolator=[Configuration] | Specify an interpolating decision procedure |
The interpolating decision procedures are used to generate predicates from spurious abstract paths.
Interpolants are generated for a specific theory (or combination of theories)
like integers, difference constraints and reals.
However, interpolants are not unique.
So that, for the same theory, results may differ across different decision procedures.
Furthermore, certain theories like integers are not supported by all
decision procedures and one has to resort to the theory of reals.
This can lead to incompleteness because certain formulas that are unsatisfiable
when interpreted over integers are satisfiable with respect to the theory of reals.
Obviously, the choice of the decision procedure can have an immediate
impact on the results produced by PASS.
PASS supports the two interpolating decsion procedures
that are being maintained and publically available at the time of this writing:
Configuration |
Description |
MathSat |
MathSat SMT solver |
CSIsat |
CSIsat interpolating decision procedure |
2.2 Value iteration
Value iteration performs an iterative numerical computation where the states in a stochastic game or a Markov decision process are updated in each iteration. Value iteration propagates probability mass in a backward direction starting from the goal states. The probability at a state depends on the probability at its successors.
2.2.1 Iteration Order
| --ValiterOrder=[Configuration] | control order of updates in value iteration |
The order in which states are updated in value iteration can be changed without destroying its convergence properties. However, it is beneficial to schedule the state updates taking dependencies between states into account, e.g., to give the successor of a state which is closer to the goal states a higher priority than the state. In this way, the probability that comes from the goal states spreads faster across the state space.
We have implemented a simple scheme, configuration rdfs,
that orders the states by performing
a depth-first search starting from the goal states.
The value iteration procedures according to this ordering.
This optimization reduces the the number of required iterations significantly
compared to the scheme that is used in, e.g., PRISM.
There the ordering does not take dependencies into account
but is instead an artifact of the state representation.
We also make this method available as configuration random.
Configuration |
Description |
rdfs |
reverse DFS order |
random |
random update order |
2.2.2 Precision
Value iteration is an approximation algorithm which guarantees convergence only in the limit. Several parameters control the precision of value iteration by giving stopping criteria.
Option |
Description |
--epsilon |
Stopping criterion for refinement (if lower and upper bound deviate by less than epsilon we stop) |
--max_iters |
Maximal number of iterations in value iteration (default 10000) |
--term_crit_param |
Numerical precision (difference below which two numbers are considered equal) |
Note
The values initialsize and finalsize do not
include the reflexive relation, which is obviously always there. This means that a final number of
pairs of zero does not mean that the relation is empty, it means that the relation is empty except
for the reflexive relation.
2.3 Output
| --Verbose | verbose mode | |
| --DumpProofScript | dump queries to SMT solver in log file | |
| --PrettyPrintModel | view model after transformations done by the frontend | |
| --SMTTypeCheck | switch on type checking in SMT solver |
3 Visualization
| --Debug | Generate graph output and do consistency checks for debugging |
PASS generates graph output for the aiSee graph layout
software from AbsInt. The layout software aiSee scales to very large graphs with thousands of nodes and is available free of charge.
m=0..2, x=k and x<k, is extracted
from the guards and the property.
The corresponding stochastic game is
depicted in the figure below.
Abstract states are shown as boxes. The boxes contain analysis information:
- the probability interval which reflects the range of probabilities of the concrete states contained in the abstract state.
- the predicates that define the abstract state.
The color of a box indicates if the state is initial (green), a goal state (red), and whether the lower and upper bound of its probability interval agree (white) or are different (gray).
Distributions are depicted by triangles.
The initial state has 6 out-going probability distributions.
They are labeled with the command that induces them.
Command a is depicted by 0 and b by 1
in the triangle.
The non-determinism between commands a and b is inherent
to the original program.
The non-determinism between distributions of the
same command is induced by uncertainty from abstraction.
PASS distinguishes between these kinds of non-determinism.
Player 1 controls original non-determinism and player 2 non-determinism from abstraction. Rather than explicitly introducing player 2 vertices, the distributions are labeled with their respective command. This simplifies the visualization and improves performance: the visualization is a direct output of the sparse-matrix data structure used for value iteration.
The lower bound probabilities for maximal probabilistic reachability are obtained by maximizing over player~1 and minimizing over player 2 decisions (sup inf) of the game and the upper bound is obtained by maximizing over all decisions (sup sup). This yields a probabilities and a strategies under which the probability is achieved. Strategies are shown by colored lines: purple if both strategies agree, blue for the lower-bound strategy, red for upper-bound strategy.
The box with the thick border is the abstract state that is refined.
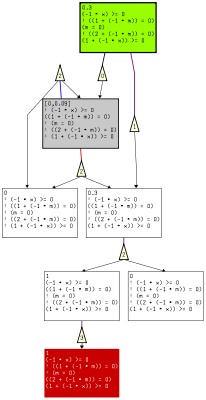
After one refinement step the abstraction looks like this:

The final precise abstraction is:


