Case Studies
Fault Trees of 3P2M
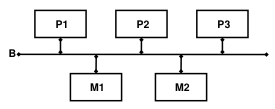
The following figure depicts a high-level model of the 3P2M system. The system consists of three identical processors (P1–P3) and two identical memory modules (M1 and M2), all connected by a bus (B). The processors and the memory modules work independently of each other, and they, together with the bus, over time fail. The failure of each component is governed by a continuous probability distribution. The system fails when either all processors fail or all memory modules fail or the bus fails.
The fault tree model of the 3P2M system is depicted in the following figure. A fault tree model consists of several basic events and gates. A basic event represents the failure of some basic, indivisible component, while a gate represents and determines the relationship and interdependency between several basic events.
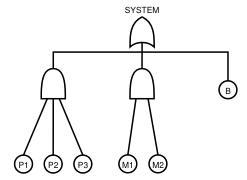
In the standard or static fault trees, there are three types of gates: OR, AND, and VOTING gates. The OR and AND gates are the standard logic gates, and they are depicted in the same way. In this case study, we illustrate the possibility of employing more complex Markovian distributions to govern the basic events. The possibility arises from the fact that OR and AND gates in the fault trees correspond exactly to the minimum and respectively maximum operations.
Let Pi denote a process describing the time to failure of processor Pi, for i = 1, 2, 3. Further, let Mi be a process describing the time to failure of memory module Mi, for i = 1, 2, and similarly with B, the process describing the time to failure of the bus B. Then the fault tree model in the previous figure can be expressed by process:
min(min(max(max(P1,P2),P3),max(M1,M2)),B) |
To analyze the reliability of the 3P2M model, we conduct several experiments. In each experiment, the time to failure of each component is governed by Erlang distributions of a particular phase (number of states). The mean value of the Erlang distributions governing each component, however, are kept the same in all experiments, which means that the rates must be adjusted accordingly. The mean failure times of each processor, each memory, and the bus are set to around 5, 3.33, and 7.14 years, respectively. The following table lists the parameters of the Erlang distributions used in the experiments.
Phases |
Processors |
Memories |
Bus |
Model |
1 |
exp(0.2) |
exp(0.3) |
exp(0.14) |
Model 1 |
5 |
erl(5, 1) |
erl(5, 1.5) |
erl(5, 0.7) |
Model 5 |
10 |
erl(10, 2) |
erl(10, 3) |
erl(10, 1.4) |
Model 10 |
20 |
erl(20, 4) |
erl(20, 6) |
erl(20, 2.8) |
Model 20 |
50 |
erl(50, 10) |
erl(50, 15) |
erl(50, 7) |
Model 50 |
100 |
erl(100, 20) |
erl(100, 30) |
erl(100, 14) |
Model 100 |
The next table summarizes the result of the experiments. We have six 3P2M models, where we vary the phases of the Erlang distributions governing the basic events, ranging from 1, which corresponds to exponential distributions, to 100. The second column of the table (Original) describes the number of states in the resulting CTMC models when they are generated without any size reduction whatsoever. The third column (Inter.) corresponds to the number of states in the largest intermediate CTMC models the reduction algorithm encounters while minimizing each of the six 3P2M models. The fourth column (Final) corresponds to the number of states in the final CTMC models. Compared to the original state spaces, the size of the final state spaces is orders-of-magnitude smaller. While the size of an original model grows multiplicatively in the sizes of its components, the size of a reduced representation grows additively in the sizes of its components.
Phases |
Original |
Intermediate |
Final |
1 |
21 |
6 |
6 |
5 |
37625 |
450 |
114 |
10 |
1596000 |
1950 |
249 |
20 |
81488000 |
8100 |
519 |
50 |
> 1.72 x 1010 |
51750 |
1329 |
100 |
> 1.05 x 1012 |
208500 |
2679 |

