Case Studies
- Boucing Ball (CAV 2010)
- Water Level Control (CAV 2010)
- Autonomous Lawn-Mower (CAV 2010)
- Thermostat (CAV 2010)
- Water Level Control (HSCC 2011)
- Temperature Control (HSCC 2011)
- Moving-block Train Control (HSCC 2011)
Bouncing Ball (CAV 2010)
We consider a bouncing ball assembled from different materials. Assume this ball consisting of three parts: 50 per cent of the its surface consists of hard material, 25 per cent consists of a material of medium hardness and the rest consists of very soft material. We drop the ball from a height h=2. Further, we assume the gravity constant to be g=1. If the ball hits the floor and falls on the hard side, it will jump up again with one half of the speed it had before, if it falls down on the medium side it will jump up with a quarter of the speed. However, if it hits the ground with its soft side, it won't jump up again. We assume that the side with which the ball hits the ground is determined randomly, according to the amount surface covered by each of the materials.
We study the probability that the ball falls on the soft side
before time bound T and consider several time bounds:
results are given in the table below. We conducted three main
analysis settings. In the left and medium part of the table, we used
partitioning with interval length of 0.15 on the position and
speed variables. For the medium part, we used
the PHAVer-specific convex hull over-approximation
[Frehse05]. For
the right part of the table, we used an
interval length of 0.05, and the convex hull
over-approximation. Entries for which the analysis did not terminate
within one hour are marked by "-".
We ascertain here that, without the convex hull over-approximation, with an interval of length 0.15, we obtain non-trivial upper bounds. However, the analysis time as well as the number of states grows very fast with increasing time bound. The reason for this to happen is, that each time the ball hits the ground, there are three possibilities with which side it will hit the ground. Thus, the number of possibilities for the amount of energy the ball still has after a of times n the ground is hit is exponential in n. Also notice that there is some time bound up to which the ball has done an infinite number of jumps in all cases, as this case study features Zeno behaviour. This indicates that for time bounds near this value we have to use very small partitioning intervals to obtain realistic probability bounds. This leads to an even larger time and memory consumption in the analysis.
If we use the convex hull over-approximation and an interval length of 0.15, far less resources have to be used. But we only obtain non-trivial results for time bounds up to 3. Using an interval width of 0.05, we obtain a tighter probability bound, while using still less resources than the first configuration. However, for time bound T=3.7 the third configuration does not terminate within one hour.
| Time bound | Interval length 0.15 | Interval length 0.15, hull | Interval length 0.05, hull | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Probability | Build (s) | Abstract states | Probability | Build (s) | Abstract states | Probability | Build (s) | Abstract states | |
| 1 | 0 | 1 | 38 | 0 | 1 | 17 | 0 | 2 | 56 |
| 2 | 0.25 | 3 | 408 | 0.25 | 2 | 59 | 0.25 | 9 | 185 |
| 3 | 0.5 | 13 | 3K | 0.5 | 4 | 124 | 0.312 | 22 | 347 |
| 3.5 | 0.5 | 70 | 11K | 1 | 5 | 145 | 0.5 | 32 | 425 |
| 3.6 | 0.5 | 140 | 14K | 1 | 6 | 150 | 0.5 | 37 | 436 |
| 3.7 | 0.5 | 214 | 18K | 1 | 6 | 154 | - | - | - |
For a time bound of three, we can compute the probability manually: the ball can hit the ground with its soft side when it hits the floor in first place with a probability of 0.25. It hits the ground initially with its hard side with a probability of 0.5. In this case, it won't hit the ground again before T=3. If it first hits the ground with its medium hard side, it will hit the ground a second time before T=3. After this, there is no change of touching the ground again before the time bound. Because of this, the overall probability of the property under consideration is 0.25 + 0.25⋅0.25 = 0.3125. This means that the result obtained by using an interval length of 0.05 and the convex hull overapproximation is exact.
Water Level Control (CAV 2010)
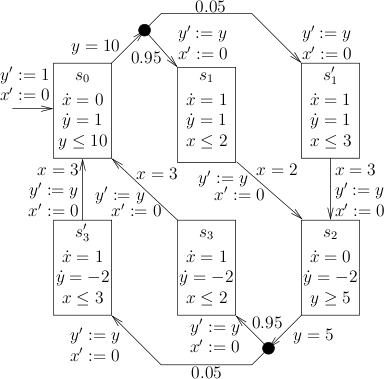
We consider a model of a water level control system (extended from the one in [Alur95].) which uses wireless sensors. Values submitted are thus subject to probabilistic delays, due to the unreliable transport medium.
A sketch of the model is given in the figure above. The water level y of a tank is controlled by a monitor. Its change is specified by a linear function. Initially, the water level is y=1. When no pump is turned on (s0), the tank is filled by a constant stream of water (ẏ). When a water level of y=10 or above is seen by a sensor of the tank, the pump should be turned on. However, the pump features a certain delay, which results from submitting control data via a wireless network. With a probability of 0.95 this delay takes 2 time units (s1), but with a probability of 0.05 it takes 3 time units (s1'). The delay is realized by the timer x. After the delay has passed, the water is pumped out with a higher speed than it is filled into the tank (ẏ=-2 in s2). Another sensor perceives whether the water level is below 5 turns pump must off again. Again, we have a distribution over delays here (s3 and s3'). For the system to work correctly, the water level must stay between a value of 1 and 12
We are interested in the probability that the pump system violates the
property given above, that is either the water level falls below 1
or grows above 12, within a given time bound T. We model the
system in ProHVer and reason about this property: performance
statistics are given in the table below. Without using
partitioning, we were only able to obtain exact values for time bounds
up to 82 including.
Notice that we did not use the
convex hull over-approximation, like in the bouncing ball case study,
nor another over-approximation.
For time bounds larger than this value, we always obtained a
probability limit of 1. To get tighter result, we partitioned x
by an interval of length 2. For time bounds below 83 we obtain
the exact value in both table parts, whereas for 83 we obtain a
useful upper bound only when using partitioning.
| Time bound | No partitioning | Interval 2 | ||||
|---|---|---|---|---|---|---|
| Probability | Build (s) | Abstract states | Probability | Build (s) | Abstract states | |
| 40 | 0.185 | 0 | 69 | 0.185 | 1 | 150 |
| 82 | 0.370 | 0 | 283 | 0.370 | 2 | 623 |
| 83 | 1 | 1 | 288 | 0.401 | 2 | 640 |
| 120 | 1 | 1 | 537 | 0.512 | 4 | 1220 |
| 500 | 1 | 38 | 3068 | 0.954 | 79 | 7158 |
| 1000 | 1 | 169 | 6403 | 0.998 | 365 | 14977 |
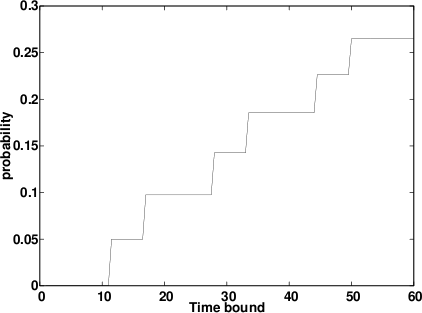
A plot of probabilities for different time bounds is given in the figure below. The graph has a staircase form where wide steps alternate with narrow ones. This form results, because each time the longer time bound was randomly chosen, the tank will overflow or underflow respectively, if there is enough time left. The wide steps corresponds to the chance of overflow in the tank, the narrow ones to the chance of underflow.
Autonomous Lawn-Mower (CAV 2010)
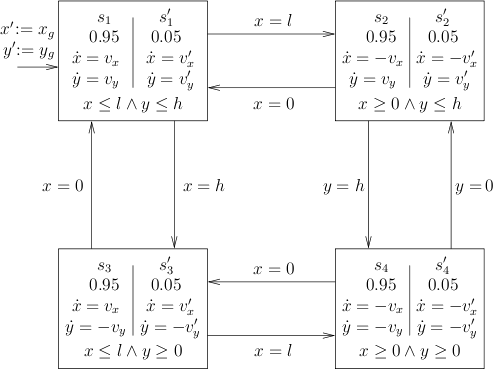
We consider an autonomous lawn-mover that uses a probability bias to avoid patterns on lawns. This mower is started on a rectangular grassed area. When it reaches the border of the area, it changes its direction. To prevent the mower from following a simple cyclic pattern, this direction is randomly biased, such as to ensure that finally the entire area has been cut.
A sketch of the automaton is given in the figure above. There, l is the length and h the width of the area. The position of the mower on the area is given by (x,y). With (vx,vy) we denote the speed in (x,y) direction, which the mower takes with a probability of 0.95 when reaching a border, whereas with (vx',vy') denotes a variation of the speed that is taken with probability 0.05. Further, (xg,yg describes the mower's initial position.
At the region with x≥90 ∧ x≤100 ∧ y≥170 ∧ y≤200 the owner of the lawn has left a tarpaulin. We are interested in the probability that within a time bound of t=120 the mower hits the tarpaulin, thereby inevitably ripping it up.
For the analysis, we set vx = 10, vy = 10, vx' = 11, vy' = 9, l = 100, h = 200, xg = 10, yg = 20. The creation of the labelled transition system for this automaton took 98 seconds whereas the computation time of the failure probability was negligible. The upper bound we obtained was 0.000281861. We did not use any interval specifications.
As in the other case studies, we also varied the time bound. Results are given in the table below. For larger time bounds the analysis time as well as the number of states grows quickly. This is due to a similar effect as in the bouncing ball case study. Each time the mower reaches a border, it may head into two different directions, which leads to a combinatorial explosion, evident by the above statistics.
We also experimented with convex hull overapproximation without interval refinement. However, the probability bounds obtained were always 1. Using interval partitioning also did not improve on this, as it only made the analyses take more time. We feel that for this case study there is not much hope of obtaining better results in resource usage. The complexity does not really live in the hybrid behaviour, but results from the excessive number of ways the mower can pass around the area. Because of this, we don't think it is possible to find an abstraction to handle this case study for larger time bounds.
| Time bound | Probability | Build (s) | Abstract states |
|---|---|---|---|
| 10 | 0 | 0.06 | 4 |
| 70 | 1.11984e-05 | 1.22 | 632 |
| 100 | 1.11984e-05 | 8.47 | 3022 |
| 110 | 0.000281861 | 65.55 | 9076 |
| 120 | 0.000281861 | 98.83 | 12660 |
| 130 | 0.000281861 | 303.40 | 25962 |
| 140 | 0.000281861 | 743.43 | 38830 |
Thermostat (CAV 2010)
We consider the thermostat example depicted in the figure below, which is extended from the one in [AlurDI06]. There are four modes: Cool, Heat, Check and Error. The latter mode models the occurrence of a failure, where the temperature sensor gets stuck at the last checked temperature. The set of variables are {t,x,T} where T represents the temperature, t represents a local timer and x is used to measure the total time passed so far. Thus, in all modes it holds that ẋ=1 and ṫ=1. In each mode there is also an invariant constraint restricting the set of state space for this mode. Invariant constraints are only for the sake of convenience and comparison with [AlurDI06].
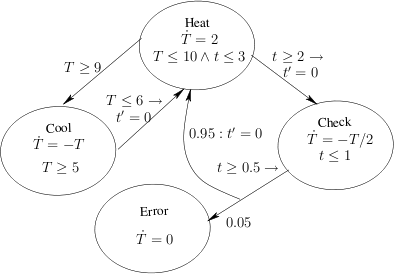
The initial condition is assumed to be m=Heat ∧ t=0 ∧ x=0 ∧ 9≤T≤10. The unsafe constraint is m=Error ∧ x≤5. We can interpret the probability of reaching the set of unsafe states as the probability of reaching the Error mode within time 5. Assume that the threshold for this risk is 0.1. In general, the verification of this property is not trivial (For the time bound 5, in a paragraph below, we show that the safety property is indeed satisfied by analysing the system analytically, and illustrate how a safe upper bound can be obtained by abstraction).
| Time bound | Interval 2 | Interval 10 | ||||
|---|---|---|---|---|---|---|
| Probability | Build (s) | Abstract states | Probability | Build (s) | Abstract states | |
| 2 | 0 | 0 | 11 | 0 | 0 | 8 |
| 4 | 0.05 | 0 | 43 | 1 | 0 | 12 |
| 5 | 0.097 | 1 | 58 | 1 | 0 | 13 |
| 20 | 0.370 | 20 | 916 | 1 | 1 | 95 |
| 40 | 0.642 | 68 | 2207 | 0.512 | 30 | 609 |
| 80 | 0.884 | 134 | 4916 | 1 | 96 | 1717 |
| 120 | 0.940 | 159 | 4704 | 0.878 | 52 | 1502 |
| 160 | 0.986 | 322 | 10195 | 0.954 | 307 | 4260 |
| 180 | 0.986 | 398 | 10760 | 0.961 | 226 | 3768 |
ProHVer can verify this property on the thermostat
within 10 seconds after building the abstract states
space. Here and in the other case studies, we only give the building
time for the abstraction of the automata, as the time to compute the
upper bounds for the reachability probabilities is negligible. In the
table above we give probability bounds and performance statistics for
different time bounds. For the left part this table, we used a
partitioning interval of length 2 but 10 for the one on
the right side for variable x. We observe that the time needed
for the analysis as well as the number of states of the abstract
transition systems grows about linearly in the time bound, though with
large oscillations. Comparing the left and the right side, we see that
for the larger interval we need less resources, as was to be
expected.
Due to the way PHAVer splits locations along intervals,
for some table entries, we see somewhat counter-intuitive
behaviour. We observe that bounds do not necessarily improve with
decreasing interval length. This is because PHAVer does
not guarantee abstractions with smaller intervals to be an
improvement, though they are in most cases. Furthermore, the
abstraction we obtain from PHAVer can not guarantee
probability bounds to increase monotonically with the time
bound. This is because a slightly increased time bound might induce
an entirely different abstraction, leading to a tighter probability
bound, and thus giving the impression of a decrease in probability,
even though the actual maximal probability indeed stays the same or
increases.
| Time bound | Interval 2 | Interval 4 | Interval 6 | Interval 8 | Interval 10 |
|---|---|---|---|---|---|
| 2 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0.05 | 1 | 1 | 1 | 1 |
| 5 | 0.097 | 0.05 | 1 | 1 | 1 |
| 20 | 0.370 | 0.337 | 0.302 | 0.302 | 1 |
| 40 | 0.642 | 0.560 | 0.512 | 0.537 | 0.512 |
| 80 | 0.884 | 0.796 | 0.796 | 0.774 | 1 |
| 120 | 0.940 | 1 | 1 | 1 | 0.878 |
| 160 | 0.986 | 0.961 | 0.954 | 0.952 | 0.954 |
| 180 | 0.986 | 0.962 | 0.958 | 0.961 | 0.961 |
In the table above we give the upper bounds for
different interval widths. An interesting observation is that, even
though smaller interval widths lead to better result on average, the
tightest bounds (in bold fonts) are obtained via different interval
widths for different time bounds. This might be due to the complicated
form of the continuous dynamics in this case study: the temperature
drops exponentially fast. In PHAVer, a new angle for the
polygon-bounded overapproximation of the reachable states is chosen at
each point a new abstract state is started due to the end of the
interval length being reached. We conjecture that in some cases when
choosing a smaller interval length, due to different angles being
selected, we include different actually unreachable behaviour. Under
unfavorable conditions, we include behaviour which allows reaching the
unsafe state with a higher probability than in the case of a larger
interval length.
It therefore seems worthwhile to explore techniques more adapted to the generation of transition systems for probabilistic hybrid automata, especially by adjusting the splitting of states to a method better adapted to our needs.
Solving the Thermostat Analytically
First we observe that the initial constraint of T is t=0 and 9≤T≤10. The system cannot stay in the mode Heat for 2 time units, as this would increase the temperature by 4 units which violates the invariant T≤10 at Heat. This means that the system must switch to mode Cool to decrease the temperature. It would take some amount of time (approximately 0.41) units to decrease the temperature until 6 such that the system can go back to Heat. Note that switching back to Heat would reset the local timer which implies that t=0 and that x≥0.41. To reach the unsafe mode Error, the intermediate mode Check must be touched. Because of the guard t≥2 between Heat and Check, once the mode Check is reached, it holds that t=0 and x≥2.41. Then, the system waits in Check at least 0.5 time units. After the probabilistic jump from Check is triggered, it holds that x≥2.91. Then, the unsafe state could be reached with probability 0.05. With probability 0.95 the system goes back to mode Heat and it holds that t=0 and x≥2.91. Reiterating the above analysis, reaching Error from Heat would again take at least 2.5 time units, which implies that there is only one chance to hit the unsafe mode Error within time 5. Thus, the probability is bounded by 0.05, which implies that the safety property is indeed satisfied.
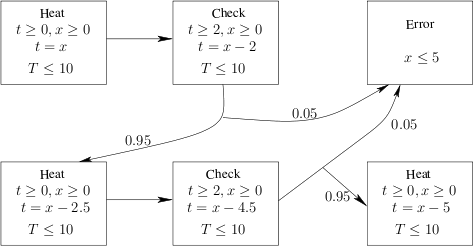
Now we consider an abstraction of the thermostat example. The initial abstract state is (Heat,B) where B represents concrete valuations satisfying the constraint t≥0, x≥0, t=x and T≤10. In the figure above we depicted fragments of the abstract states and of those abstract transitions which lead to abstract unsafe states. Notably, in this abstraction there are two chances to touch abstract unsafe states, thus the probability amounts to 0.05 + 0.95⋅ 0.05=0.0975. The reason is that from the initial state Heat the abstract automaton does not need go back to Cool to let the temperature decrease, instead it can immediately switch to Check. This is due to the over-approximation of the abstract initial states. However, the computed probability for the threshold 0.1 is still good enough to prove the safety property. If instead the threshold were set between 0.05 and 0.0975, refinement would have been needed.
Water Level Control (HSCC 2011)
Notice: The resulting probabilities may be different than the
ones in the paper for this model. The reason is that we
manually inserted the precise values in the .graph
files generated by the modified version of PHAVer which
serve as input for ProHVer.
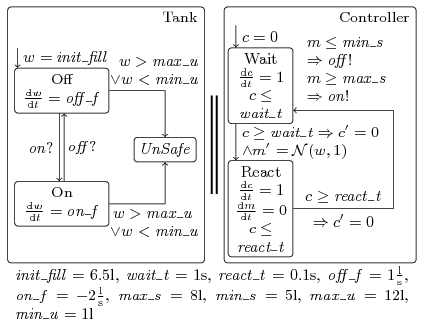
We consider a model of a water level control system (extended from the one of Alur et al. [Alur95] and our previous paper [ZhangSRHH10]). In particular, we use this case study to demonstrate the influence which different abstractions of the same continuous stochastic command have. The abstraction of a guarded command with a continuous probability distribution into one with a discrete probability distribution is described in a recent publication [FraenzleHHWZ11]. A water tank is filled by a constant stream of water, and is connected to a pump which is used to avoid overflow of the tank. A control system operates the pump in order to keep the water level within predefined bounds. The controller is connected to a sensor measuring the level of water in the tank. A sketch of the model is given in the figure above. The state "Tank" models the tank and the pump, and w is the water level. Initially, the tank contains a given amount of water. Whenever the pump is turned off in state "Off", the tank fills with a constant rate due to the inflow. Conversely, more water is pumped out than flows in when the pump is on.
The controller is modelled by automaton "Controller". In state "Wait", the controller waits for a certain amount of time. Upon the transition to "React", the controller measures the water level. To model the uncertainties in measurement, we set the variable m to a normal distribution with expected value w (the actual water level) and standard deviation 1. According to the measurement obtained, the controller switches the pump off or on.
We are interested in the probability that within a given time bound,
the water level leaves the legal interval. In the table below,
we give upper bounds for this probability for different time bounds as well as
the number of states in the abstraction computed by PHAVer and the
time needed for the analysis. For the stochastic guarded command
simulating the measurement, we consider different abstractions by
probabilistic guarded commands of different precision, for which we
give the abstraction functions in the table caption. When we refine
the abstraction A to a more precise B, the probability bound
decreases. If we introduce additional non-determinism as in
abstraction C, probabilities increase again. If we refine B again
into D, we obtain even lower probability bounds. The price to be
paid for increasing precision, however, is in the number of abstract
states computed by PHAVer as well as a corresponding increase in the
time needed to compute the abstraction.
| time bound | Abstraction A | Abstraction B | Abstraction C | Abstraction D | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| prob. | build (s) | states | prob. | build (s) | states | prob. | build (s) | states | prob. | build (s) | states | |
| 20s | 0.1987 | 3 | 999 | 0.0982 | 3 | 1306 | 0.1359 | 3 | 1306 | 0.0465 | 5 | 1920 |
| 30s | 0.2830 | 6 | 2232 | 0.1433 | 8 | 2935 | 0.1870 | 8 | 2935 | 0.0693 | 15 | 4341 |
| 40s | 0.3580 | 16 | 3951 | 0.1860 | 18 | 5212 | 0.2547 | 18 | 5212 | 0.0916 | 47 | 7734 |
| 50s | 0.4250 | 34 | 6156 | 0.2264 | 42 | 8137 | 0.3024 | 43 | 8137 | 0.1134 | 108 | 12099 |
| 60s | 0.4848 | 67 | 8847 | 0.2647 | 86 | 11710 | 0.3577 | 85 | 11710 | 0.1347 | 219 | 17436 |
Manual analysis shows that in this case study, the over-approximation of the probabilities only results from the abstraction of the stochastic guarded command into a probabilistic guarded command and is not increased further by the state-space abstraction.
- model file, abstraction A
- model file, abstraction B
- model file, abstraction C
- model file, abstraction D
Temperature Control (HSCC 2011)
Notice: The resulting probabilities may be different than the
ones in the paper for this model. The reason is that we
manually inserted the precise values in the .graph
files generated by the modified version of PHAVer which
serve as input for ProHVer.
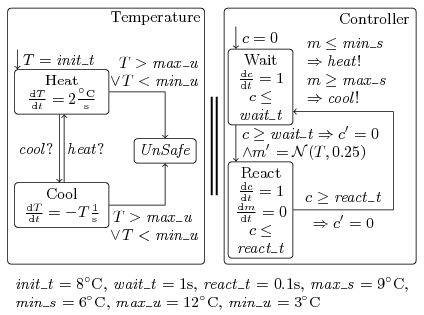
We consider a temperature control system extended from a previous case
study [ZhangSRHH10], originally studied by Alur et
al. [AlurDI06].
In this model, continuous distributions are used.
The abstraction of a guarded command with a continuous probability
distribution into one with a discrete probability distribution is
described in a recent publication [FraenzleHHWZ11].
In the figure above we depict the
system structure. We ask whether using an air
conditioning control system we are able to keep the temperature of a
room within a certain range. In contrast to the water level case study,
we use a non-linear model of the temperature evolution, and instead of
varying the splitting of the normal distribution, we vary the refine
interval used by PHAVer to analyse non-linear hybrid systems. A
smaller refine interval leads to a more precise abstraction of the
state-space.
| time bound | interval length ∞ | interval length 2 | interval length 1 | interval length 0.5 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| prob. | build (s) | states | prob. | build (s) | states | prob. | build (s) | states | prob. | build (s) | states | |
| 2s | 1 | 0.03 | 7 | 0 | 0.17 | 16 | 0 | 0.21 | 21 | 0 | 0.30 | 31 |
| 4s | 1 | 0.05 | 23 | 1 | 1.26 | 269 | 0.284643 | 1.61 | 316 | 0.284643 | 2.97 | 546 |
| 6s | 1 | 0.07 | 39 | 1 | 5.79 | 1518 | 0.360221 | 8.66 | 2233 | 0.360221 | 17.39 | 3797 |
| 8s | 1 | 0.10 | 55 | 1 | 19.27 | 4655 | 1 | 35.62 | 8261 | 0.488265 | 81.39 | 16051 |
| 10s | 1 | 0.12 | 71 | 1 | 53.25 | 10442 | 1 | 119.33 | 20578 | 0.590683 | 507.12 | 44233 |
In the table above,
we give probability bounds and performance statistics. We used a
refine interval on the variable T which models the temperature. The
interval lengths are given in the table. For all instances there is an
interval length small enough to obtain a probability bound that is the
best possible using the given abstraction of the normal
distribution. Smaller intervals were of no use in this case. The
drastic discontinuities in probability bounds obtained are a
consequence of non-linearity, and abstraction by PHAVer.
Moving-block Train Control (HSCC 2011)
Notice: The resulting probabilities may be different than the
ones in the paper for this model. The reason is that we
manually inserted the precise values in the .graph
files generated by the modified version of PHAVer which
serve as input for ProHVer.
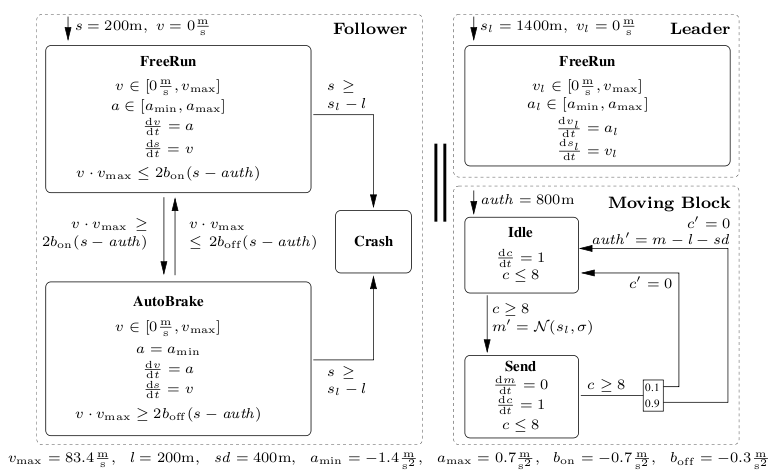
We present a model of headway control in the railway domain, as depicted in the figure above. In this case study, continuous distributions are used. The abstraction of a guarded command with a continuous probability distribution into one with a discrete probability distribution is described in a recent publication [FraenzleHHWZ11]. A more extensive description of the setting plus a closely related case study containing a sampling-related bug not present in the current model appeared in a different publication [HerdeEFT08]. In contrast to fully automated transport, which is in general simpler to analyse (as the system is completely under control of the embedded systems) our sample system implements safe-guarding technology that leaves trains under full human control provided safety is not at risk. It is thus an open system, giving rise to the aforementioned analysis problems.
Our model implements safe interlocking of railway track segments by means of a "moving block" principle of operation. While conventional interlocking schemes in the railway domain lock a number of static track segments in full, the moving block principle enhances traffic density by reserving a "moving block" ahead of the train which moves smoothly with the train. This block is large enough to guarantee safety even in cases requiring emergency stops, i.e. has a dynamically changing block-length depending on current speed and braking capabilities. There are two variants of this principle, namely train separation in relative braking distance, where the spacing of two successive trains depends on the current speeds of both trains, and train separation in absolute braking distance, where the distance between two trains equals the braking distance of the second train plus an additional safety distance (here given as sd=400m). We use the second variant, as also employed in the European Train Control System (ETCS) Level 3.
Our simplified model consists of a leader train, a follower train, and a moving-block control regularly measuring the leader train position and communicating a related movement authority to the follower. The leader train is freely controlled by its operator within the physical limits of the train, while the follower train may be forced to controlled braking if coming close to the leader. The control principle is as follows:
- 8 seconds after communicating the last movement authority, the moving-block control takes a fresh measurement m of the leader train position sl. This measurement may be noisy.
- Afterwards, a fresh movement authority derived from this measurement is sent to the follower. The movement authority is the measured position m minus the length l of the leader train and further reduced by the safety distance sd. Due to an unreliable communication medium, this value may reach the follower (in which case its movement authority auth is updated to m-l-sd) or not. In the latter case, which occurs with probability 0.1, the follower's movement authority stays as is.
-
Based on the movement authority, the follower continuously
checks the deceleration required to stop exactly at the movement
authority. Due to
PHAVerbeing confined to linear arithmetic, this deceleration is conservatively approximated as areq = (v⋅vmax) / (2(s-auth)), where v is the actual speed, vmax the (constant) top speed, and s the current position of the follower train, rather than the physically more adequate, yet non-linear, areq = v2/(2(s-auth)) of the original model [HerdeEFT08]. - The follower applies automatic braking whenever the value of areq falls below a certain threshold bon. In this case, the follower's brake controller applies maximum deceleration amin, leading to a stop before the movement authority as amin < bon. Automatic braking ends as soon as the necessary deceleration areq exceeds a switch-off threshold boff > bon. The thresholds bon and boff are separate to prevent the automatic braking system from repeatedly engaging and disengaging in intervals of approximately 8 seconds when the leading train is moving.
| time bound | Abstraction A | Abstraction B | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| probability (σ = 10, 15, 20) | build (s) | states | probability (σ = 10, 15, 20) | build (s) | states | |||||
| 60s | 7.110E-19 | 6.215E-09 | 2.141E-05 | 65 | 571 | 1.806E-06 | 2.700E-03 | 3.847E-02 | 62 | 571 |
| 80s | 1.016E-18 | 8.879E-09 | 3.058E-05 | 201 | 1440 | 2.580E-06 | 3.855E-03 | 5.450E-02 | 183 | 1440 |
| 100s | 1.219E-18 | 1.066E-08 | 3.669E-05 | 470 | 2398 | 3.096E-06 | 4.624E-03 | 6.504E-02 | 472 | 2392 |
| 120s | 1.524E-18 | 1.332E-08 | 4.587E-05 | 1260 | 4536 | 3.870E-06 | 5.777E-03 | 8.063E-02 | 1210 | 4524 |
| 140s | 1.727E-18 | 1.509E-08 | 5.198E-05 | 2541 | 6568 | 4.386E-06 | 6.544E-03 | 9.088E-02 | 2524 | 6550 |
| 160s | 2.031E-18 | 1.776E-08 | 6.116E-05 | 5764 | 10701 | 5.160E-06 | 7.695E-03 | 1.060E-01 | 5700 | 10665 |
We consider the probability to reach the state "Crash" in which
the follower train has collided with the leader train. In
the table above, we give probability
bounds and performance results. We modelled the measurement error
using a normal distribution with expected value sl,
i.e. the
current position of the leader train. In the table, we considered
different standard deviations of the measurement. The abstraction used
for each of them can be obtained using structurally equal Markov
decision processes, only with different probabilities. Thus, we only
needed to compute the abstraction once for all deviations, and just
had to change the transition probabilities before obtaining
probability bounds from the abstraction. It was sufficient to split
the normal distribution into two parts. Depending on where we set the
split-point, we obtained probability bounds of different
quality. Although this hybrid automaton is not linear, such that
PHAVer needs to over-approximate the set of reachable states,
we are
still able to obtain useful probability bounds when using an adequate
abstraction, without refine intervals.
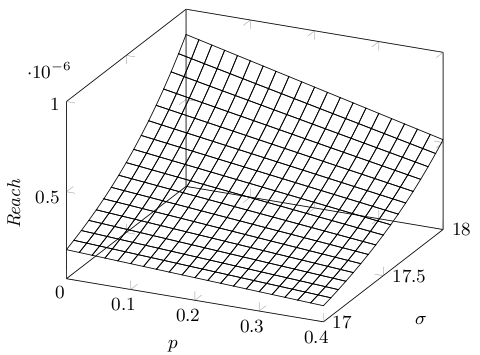
The graph in the figure below
reveals the expected positive correlation between measurement error
and risk, but also the effectiveness of the fault-tolerance mechanism
handling communication loss. Here, bounds for probability of crash
are given as a function of probability of movement authority loss
p and standard deviation σ of the
distance measurement. A time bound of 100s and Abstraction A
was used. We see that crashes due to communication
losses are effectively avoided, rooted in the principle of maintaining
the last received movement authority whenever no fresh authority is at
hand. In fact, risk correlates negatively with the likelihood of
communication loss. The function correlating risk to measurement error
and probability of communication loss has been computed by the tool
PARAM [HahnHWZ10].