INFAMY
Tools Overview Contact Us Publications Case Studies Home

Case Studies

Below are a number of case studies conducted using INFAMY. Most of them are variants of case studies from the PRISM homepage. All of them are based on them described in the publications section. The results were obtained on a Linux machine with an AMD AthlonTM XP 2600+ processor at 2 GHz equipped with 2 GB of RAM. Where convenient, we denote multiples of thousand by "K".

Random Walk

We consider a discrete-space, continuous-time random walk model, in which a walker starts from the initial position 0, and changes position with rate λ. The field directly left to the current position is chosen with a probability of p, and the field to the right with a probability of 1-p. We consider two properties:

  1. an instantaneous reward property: the expected distance from the starting point at a given point in time
  2. a probabilistic reachability property: the probability that the walker moves at least 10 fields to the right within a certain time bound t, expressed by P=? (♢≤t m≥10) where m denotes the position of the walker.

The corresponding results for p=0.25, and λ=1 are given in the table below. For the truncation, a precision of 10-6 was used. Here, the analysis time given is only for analyzing the first property after state-space exploration. The time with respect to the second property is in the same order as the first one. As apparent from the data, the size of the model is approximately proportional to the depth and the time bound t. The Layered-chain and FSP configurations achieve consistently smaller truncation depths than Uniform. Due to the simple structure of the model, however, FSP turns out to be slower than the Uniform and Layered chain configurations. This is because, for the FSP configuration, the transient analysis for state exploration consumes a proportionally high amount of time, especially for large time bounds t.

Random walk statistics.
t Uniform Layered FSP exp. prob.
dep time (s) n dep time (s) n dep time (s) n
50 223 0.9/0.0 447 71 0.9/0.0 143 62 0.9/0.0 125 2.50E+01 0.99
100 273 0.9/0.0 547 121 0.9/0.0 243 101 1.0/0.0 203 5.00E+01 1.00
1K 1.3K 0.9/0.1 2.5K 885 0.9/0.1 1.8K 654 16.3/0.0 1.3K 5.00E+02 1.00
5K 5.6K 0.9/1.8 11.2K 4.0K 1.2/1.2 8.1K 2.8K 1,462/0.7 5.7K 2.50E+03 1.00

Jackson Queuing Networks

A Jackson Queuing Network (JQN) [Jackson57] is a system consisting of a number of n interconnected queuing stations. A JQN with two queues is depicted in the figure below.

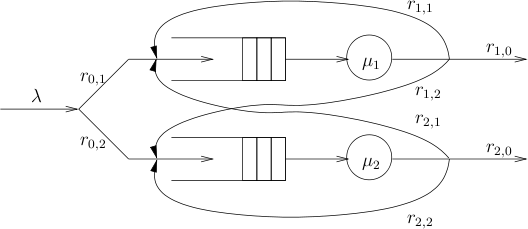
A JQN with two queues

Jobs arrive from the environment with a negative exponential inter-arrival time and are distributed to station i with probability r0,i. Each station is connected to a single server which handles the jobs with a service time given by a negative exponential distribution with rate μi. Jobs processed by the station of queue i leave the system with probability ri,0 but are put back into queue j with probability ri,j. JQNs have an infinite state space because the queues are unbounded. Initially all queues are empty. In this paper, we consider JQN models with N=3,4,5 queues. The arrival rate for N queues is λ, which is then distributed to station j (with service rate μj:=j) with probability μj/(∑i=1Nμi). The probability out of a service rate is then uniformly distributed. We compute the probability that, within t=10 time units, a state is reached in which 4 or more jobs are in the first and 6 or more jobs are in the second queue.

JQN with N queues and arrival rate λ
N/λ Uniform Layered FSP prob.
dep time n dep time n dep time n
3 / 2 193 8/19 1,236K 46 1/1 18K 37 4/0 10K 1.98E-01
4 / 2 - - - 46 3/11 230K 35 43/4 82K 1.20E-01
5 / 2 - - - 46 37/187 2,349K 34 392/50 576K 8.94E-02
3 / 3 203 10/23 1,436K 60 1/1 40K 51 14/1 25K 5.90E-01
4 / 3 - - - 60 7/27 635K 48 202/13 271K 4.42E-01
5 / 3 - - - - - - 46 2,299/193 2,349K 3.71E-01
3 / 4 212 12/26 1,633K 74 1/2 73K 64 35/1 48K 8.38E-01
4 / 4 - - - 74 15/55 1,426K 61 665/29 677K 7.16E-01
3 / 5 223 13/31 1,898K 88 2/3 121K 77 76/2 82K 9.43E-01
4 / 5 - - - 88 30/101 2,794K 74 1,772/58 1,426K 8.65E-01

Results for different number of queues N and arrival rate λ are given in the table above. For the truncation, a precision of 10-6 was used. Observe that, for fixed arrival rate λ, the depth is insensitive to the number of queues in Layered and Uniform configurations. The service rate increases with N, however, transitions corresponding to the service rate only lead back to states which are already explored, thus not contributing to the forward exit rates. For FSP, the depth is smaller than the Layered chain configuration. The number of states, and also the number of transitions, grow very fast with respect to the depth. Uniform chain cannot handle the cases N=4,5, as opposed to the other two configurations. While in the Layered chain configuration the dominating part is the model checking time in the truncation, the dominating part of the FSP configuration is the state exploration part. For N=5 and λ=3;, it is the only configuration that still works.

If the truncation grows very fast with respect to the depth, an approach that combines the two configurations might be the only option for large N and λ. Such an approach is left for future work.

Quasi-Birth-Death Processes

In [KatoenKLW07], a case study is considered that describes a system consisting of a fixed number of m processors and an infinite queue for storing job requests. The processing speed of a processor is described by the rate γ, while λ describes the incoming rate of new jobs. If a new job arrives while at least one processor is idle, the job will be processed directly. Otherwise, it will be put into a waiting queue. If there are idle processors and the waiting queue is non-empty, a job will be taken from the queue and processed immediately. To model this spontaneous transition, a rate μ >> λ is used. The stochastic Petri net (SPN) used in [KatoenKLW07]is depicted in the figure below for the case m=3.

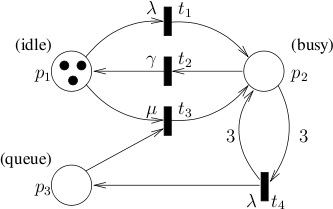
Quasi-Birth-Death Process

Tokens in place p1 represent the number of idle processors, place p2 describes the number of busy processors and place p3 gives the number of jobs in the queue. Transition t1 models the case of an incoming job given that at least one processors is idle, whereas t4 describes the case in which all processors are busy, thus the job is put into the queue. Transition t2 represents the successful termination of a job. Finally, t3 is the spontaneous transition in case there are idle processors and the queue is non-empty. We consider the probability that, given that all processors are busy and there are no jobs in the queue, within t time units a state will be reached in which all processors are idle and the queue is empty. We can compute the probability by setting p1=0, p2=3, p3=0 as the initial state and checking the formula P=?(♢≤t p1=3 ∧ p3=0).

Quasi-Birth-Death Process
λ Uniform Layered FSP exponential prob.
depth time (s) n depth time (s) n depth time (s) n
40 609 0.9/1.2 2,434 533 0.9/1.1 2,130 512 2.8/1.3 2,046 4.22E-04
60 846 0.9/1.6 3,382 754 0.9/1.5 3,014 1,024 4.9/2.1 4,094 1.25E-04
80 1,077 0.9/2.1 4,306 971 0.9/1.9 3,882 1,024 4.9/2.0 4,094 5.27E-05
100 1,305 0.9/2.5 5,218 1,187 0.9/2.4 4,746 2,048 9.3/4.0 8,190 2.70E-05

Results for different λ are given in the table above for μ=1000, m=3, t=10. The precision used in the truncation computation was 10-6. The uniformization rate of the underlying CTMC is 1000+λ. With the increase of λ, the depth grows approximately linearly. Thus, the performance of the FSP configuration suffers from the high cost of repeated transient analysis, and, therefore, does not terminate within two hours. As observed by Munsky [MunskyK06] this problem can be alleviated by adding more than one layer at each step. We consider a variant in which we double the number of layers we add per step, thus computing an error estimate every 1,2,4,8,... layers. We call this configuration FSP exponential. In contrary to FSP, FSP exponential configuration works reasonable. It is however not competitive with the Uniform or Layered configuration in time and memory.

Protein Synthesis

We analyze an SPN model of protein synthesis [GossP98] as depicted in the figure below.

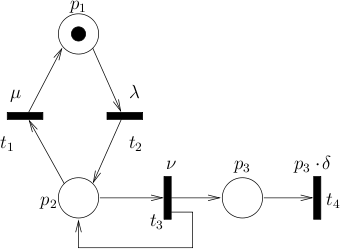
Protein Synthesis

In biological cells, each protein is encoded by a certain gene. If the gene is active, the corresponding protein will be synthesized. Also, proteins may degenerate and thus disappear after a time. Activation and deactivation of genes, protein synthesis (in case of active gene) as well as protein degeneration are modeled by stochastic rates. In the model, the place p1 corresponds to an inactive gene encoding the protein, p2 corresponds to an active gene, and p3 gives the numbers of existing proteins. The transition t1 deactivates the gene with rate μ, while t2 activates it with rate λ. If the gene is active, t3 can produce new proteins with rate ν. Each individual protein degenerates with rate δ, which is modeled by the transition t4. We consider the property that, within time t but later than 10 time units, a state is reached, in which 20 or more proteins exist and the gene is inactive: P=? (♢[10,t] p3 ≥ 20 ∧ inactive) where inactive is an atomic proposition representing inactive genes.

Protein synthesis
t Uniform Layered FSP prob.
depth time (s) n depth time (s) n depth time (s) n
300 2,330 0.9/2.0 4,659 2,047 0.9/1.7 4,093 34 1.0/0.0 67 2.07E-02
500 3,636 0.9/7.8 7,271 3,308 1.0/6.4 6,615 35 1.0/0.0 69 4.39E-02
1000 6,830 0.9/74.5 13,659 6,420 1.4/68.0 12,839 36 1.2/0.0 71 9.99E-02
2000 13,103 1.0/567.0 26,205 12,577 2.7/502.2 25,153 37 1.4/0.0 73 2.02E-01

The results for λ=1, μ=5, ν=1, δ=0.02 are presented in the table above. Here, for the computation of the truncation point we used a precision of 10-6 In this case study, the sum of the out-going rates of a state mainly depends on p3⋅δ. Thus the model is rate-unbounded. On newly explored states where p3 is higher, the uniformization rate could also be increased. Thus, in or initial paper [ZhangHHW08] only time bounds t≤45 can be handled. Since in the Uniform and Layered chain configurations only forward exit rates are considered, very large time bounds can now be handled. Remarkably, the depth grows very slowly with respect to time if FSP is used. Even though global rates are unbounded, this is of no consequence, since most of the rates lead back to states at lower depth. This also means that the probability of going out is very small. Both Uniform and Layered chain configuration do not exploit this. Thus the resulting truncation depth is significantly higher.

Grid-World Robot

We consider a grid world in which a robot moves from the lower left to the upper right corner sending signals to a station [Younes05a]. A janitor moves around and may block the robot for some time. In contrast to [Younes05a], the janitor can leave the N×N field of the robot, which leads to an infinite state space. We check the property "The probability that the robot reaches the upper right corner of the field within 100 time units while maintaining a probability of at least 0.5 of communicating periodically (every seven minutes) with a base station, is at least 0.9", which can be expressed via the CSL formula P≥0.9 ( ( P≥ 0.5 ♢≤ 7 communicate ) U≤100 upperright ). In the table below, we give results for different N. Using the FSP method is advantageous, as each layer of the model contains quite a large number of states, and FSP only needs to explore a fraction of the layers compared to the other methods. As seen from the "prob." column, for N=2,3 the property holds, while, for N=4, it does not. The reason for the decreasing probability is that the distance the robot has to travel increases with n. Thus the probability decreases that the robot will complete its travel in time. In this case study, an implicit representation of the transitions of the model is used to avoid running out of memory. During the analysis, each time we visit a state, we compute its outgoing transitions on the fly. Afterwards, these transitions are removed and the next state is considered. The trade-off of this representation is the increasing runtime.

Grid Worlds Robot
N Uniform Layered FSP prob.
depth time (s) n depth time (s) n depth time (s) n
2 912 35/16K 9,960K 576 14/6K 3,969K 31 59/12 11K 9.99E-01
3 912 58/35K 16,563K 576 26/13K 6,591K 31 91/22 17K 9.01E-01
4 912 79/51K 23,137K 576 34/19K 9,194K 32 126/32 24K 8.95E-01

Tandem Queueing Network

This model [HermannsMS99] consists of two interconnected queues with capacity c. We consider the probability that the first queue becomes full before time 0.23. Larger time bounds are left out, since then this probability is one. The performance results for INFAMY using configuration Layered are better, while for large time bound (t≥ 1) the whole model will be explored thus PRISM will perform better.
c PRISM Layered prob.
depth time n depth time n
511 1,535 3.7/49.7 523,776 632 6.8/7.5 235,339 3.13E-02
1023 3,071 13.7/380.3 2,096,128 1,167 3.6/49.6 714,306 4.24E-03
2047 6,143 69.3/3,068.3 8,386,560 2,198 10.0/297.8 2,449,798 9.87E-05
4095 12,287 560.9/31,386.5 33,550,336 4,209 27.4/2,889.8 8,899,113 7.06E-08

Workstation cluster

While the previously discussed case studies lead to infinite CTMCs, we now assess our method on finite-state models. To compare against a model checker which does not employ truncation, we use PRISM [HintonKNP06] in version 3.2, which was latest when handling this case study.

We consider the dependability of a fault-tolerant workstation cluster [HaverkortHK00]. The figure below depicts a dependable cluster of workstations. The cluster consists of two sub-clusters, which, in turn, contain N workstations connected via a central switch. The two switches are connected via a backbone. Each component of the system can break down, and is then fixed by a single repair unit responsible for the entire system. Hereby, the quality of service (QoS) constraint

A dependable cluster of workstations

Minimum requires at least k (k < N) workstations to be operational where k=⌊¾N⌋. Workstations have to be connected via switches. If in each sub-cluster the number of operational workstations is smaller than k the backbone is required to be operational to provide the required service. We consider two properties:

  1. P=? (♢[0,1] ¬Minimum): the probability that the QoS drops below minimum quality within one time unit.
  2. the expected number of repairs by time point one. The corresponding property on the PRISM website is R=?[C<=T].

For both properties, we compare PRISM with INFAMY. The results are given in the table below. Because the resulting probabilities are very small in some cases, we use a precision of 10-12 here, for the computation of the truncation point. Results for INFAMY are given for the Layered chain and FSP configurations respectively. The Uniform chain configuration is omitted, as it is always dominated by the Layered chain configuration. PRISM implements three different engines: a sparse-matrix and two symbolic engines. We used the sparse-matrix engine as it was the fastest one.

Cluster performance statistics (both properties)
N PRISM Layered FSP prob./exp.
dep tm (s) n dep tm (s) n dep tm (s) n
512 1029 12/197/952 9466K 105 2/5/5 193K 20 2/0/0 6K 5.96E-08/0.72
1024 2053 48/1132/- 37806K 109 2/5/5 208K 26 3/0/0 11K 6.01E-08/1.08
2048 - - - 116 2/6/6 236K 36 6/1/1 22K .07E-08/1.38
4096 - - - 129 3/7/8 293K 53 19/1/1 48K 6.11E-08/1.56

In the table above, the time columns "tm (s)" have the format t1/t2/t3 where the first number t1 denotes the time needed for model construction, t2 for the time to check property 1 and t3 that for property 2. While the number of states and transitions for PRISM increases dramatically with parameter N, INFAMY scales much better in both configurations. The reason is apparent from the column displaying the depth: the depth of the full model is approximately linear in N, while the depth needed is sub-linear in N. For N≥2048 and N≥1024 respectively, PRISM cannot model check these properties as it runs out of memory and crashes; this is denoted by "-". As N increases, the truncation depth grows only slowly in INFAMY and hence, only a small fraction of the state space needs to be explored in the truncated construction. Although the FSP configuration is not very effective in terms of the total time, thereby spending the largest part of the running time in the first phase, it shows a lot of potential in terms of depth and number of states. In the table below, we give additional performance measures for a model of N=512 workstations for property 1 for larger time bounds. Results are given for PRISM (sparse engine), FSP and FSP exponential respectively. The state space explored by PRISM has depth 1029 and includes 9.4 million states. Up to t=20, INFAMY with FSP is faster than PRISM. However, for larger time bounds, the model construction time dominates, as for each layer exploration the error estimate is recomputed. The FSP variant with exponential layer explorations is suitable for this case, and is consistently the fastest method for t≤ 50, as shown in the last column of the table.

Cluster performance statistics for different time bounds.
t PRISM FSP FSP exponential prob.
time (s) depth time (s) n depth time (s) n
10.0 11.9/359.5 52 47.5/3.0 46K 64 6.8/4.7 71K 3.79E-06
20.0 11.7/593.8 80 318.1/13.5 111K 128 44.4/35.6 289K 1.01E-05
30.0 11.7/802.2 104 1,016.9/32.5 190K 128 62.5/50.2 289K 1.68E-05
50.0 11.7/1171.8 147 4,660.4/103.7 382K 256 404.9/323.0 1,167K 3.04E-05

Valid XHTML 1.1 Valid CSS! Powered by PHP